Faster Algorithms for Growing Collision-Free Convex Polytopes in Robot Configuration Space
Abstract
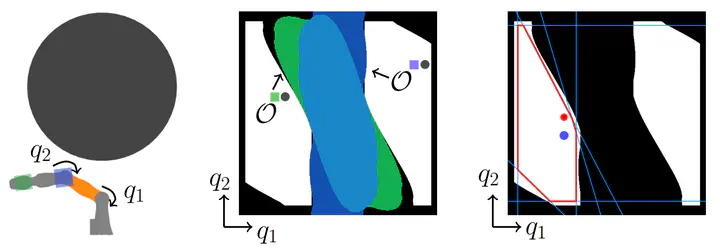
We propose two novel algorithms for constructing convex collision-free polytopes in robot configuration space. Finding these polytopes enables the application of stronger motion-planning frameworks such as trajectory optimization with Graphs of Convex Sets [1] and is currently a major roadblock in the adoption of these approaches. In this paper, we build upon IRIS-NP (Iterative Regional Inflation by Semidefinite & Nonlinear Programming) [2] to significantly improve tunability, runtimes, and scaling to complex environments. IRIS-NP uses nonlinear programming paired with uniform random initialization to find configurations on the boundary of the free configuration space. Our key insight is that finding near-by configuration-space obstacles using sampling is inexpensive and greatly accelerates region generation. We propose two algorithms using such samples to either employ nonlinear programming more efficiently (IRIS-NP2 ) or circumvent it altogether using a massively-parallel zero-order optimization strategy (IRIS-ZO). We also propose a termination condition that controls the probability of exceeding a user-specified permissible fraction-in-collision, eliminating a significant source of tuning difficulty in IRIS-NP. We compare performance across eight robot environments, showing that IRIS-ZO achieves an order-of-magnitude speed advantage over IRIS-NP. IRISNP2, also significantly faster than IRIS-NP, builds larger polytopes using fewer hyperplanes, enabling faster downstream computation.